Voici une vidéo que vous pouvez télécharger en format haute résolution, gratuitement. La vidéo est aussi sur YouTube, pour celles et ceux qui ne peuvent télécharger le gros fichier.

Si vous appréciez ce travail, je vous invite à vous inscrire à ma page Patreon. Vous m’aiderez ainsi à créer et à partager davantage de nouveaux projets. Vous y trouverez présentement une autre vidéo haute résolution que les inscrit·e·s peuvent télécharger en exclusivité, et d’autres vidéos suivront plus tard.

Contexte

J’ai réalisé beaucoup d’animations comme celle-ci ces dernières années, simplement pour mon propre plaisir, et je trouve toujours que partager de tels travaux sur les réseaux sociaux est une expérience insatisfaisante, en raison de la mauvaise qualité des vidéos recompressées. J’aime me perdre dans les petits détails de ces animations, et cette expérience ne peut se vivre sur Twitter ou sur Instagram. Même sur YouTube et Vimeo la qualité n’est pas à la hauteur du fichier original. Je ne voudrais personnellement pas regarder mon travail sur une plateforme de streaming, et inviter d’autres personnes à le faire ne me semble pas idéal.

élanger des idées mathématiques et des idées artistiques m’apporte beaucoup de joie, et conséquemment je suis toujours à la recherche de nouvelles expérimentations qui peuvent me permettre de me familiariser intuitivement avec divers concepts mathématiques. Il y a quelques semaines, j’ai regardé une vidéo YouTube de Toby Hendy, une éducatrice spécialisée en mathématiques et en physique. Elle y explique comment dessiner une parabole en utilisant une métaphore inspirée de Bob Ross, feu présentateur de l’émission de télévision The Joy of Painting.

Dans la métaphore d’Hendy, nous peignons un paysage qui contient un horizon, une montagne et un champignon situé près du sommet de la montagne.

Hendy explique qu’il nous est possible de définir spatialement le contour de la montagne en connaissant uniquement la position de l’horizon et celle du champignon. Elle dessine ensuite cette montagne avec projetant des lignes droites qui descendent verticalement de l’horizon et qui rejoignent des lignes projetées à divers angles depuis le champignon. Une parabole apparaît finalement aux endroits où se rejoignent ces lignes.

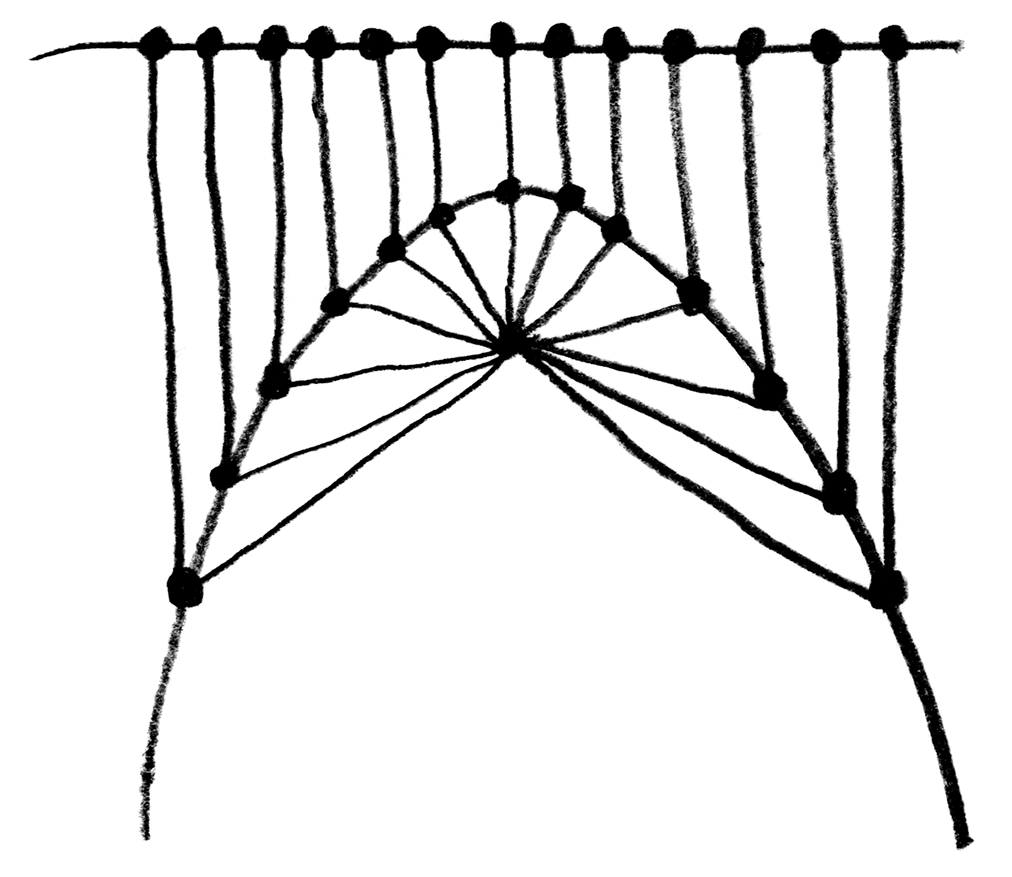
En voyant cette parabole apparaître, je n’étais pas certain de comprendre exactement ce qui s’était passé. J’ai donc décidé de recréer cette expérience avec une animation programmée à l’aide de p5.js. Voici ce que j’ai obtenu : Vous pouvez consulter le code de cette animation dans l’éditeur Web p5.js.

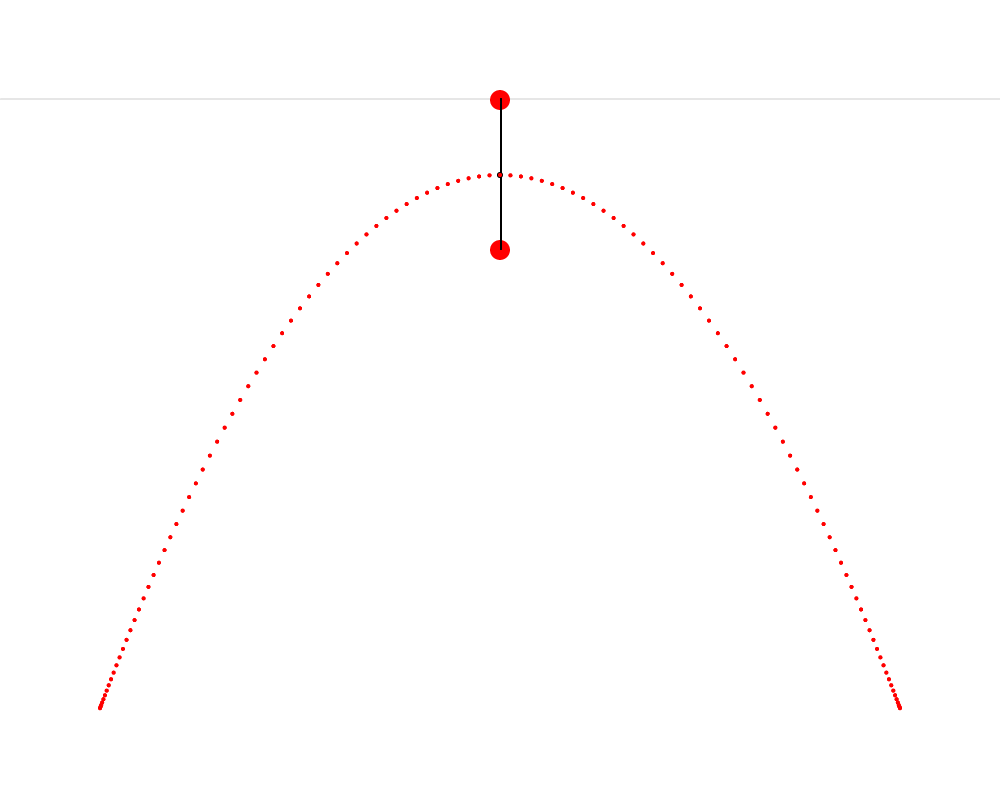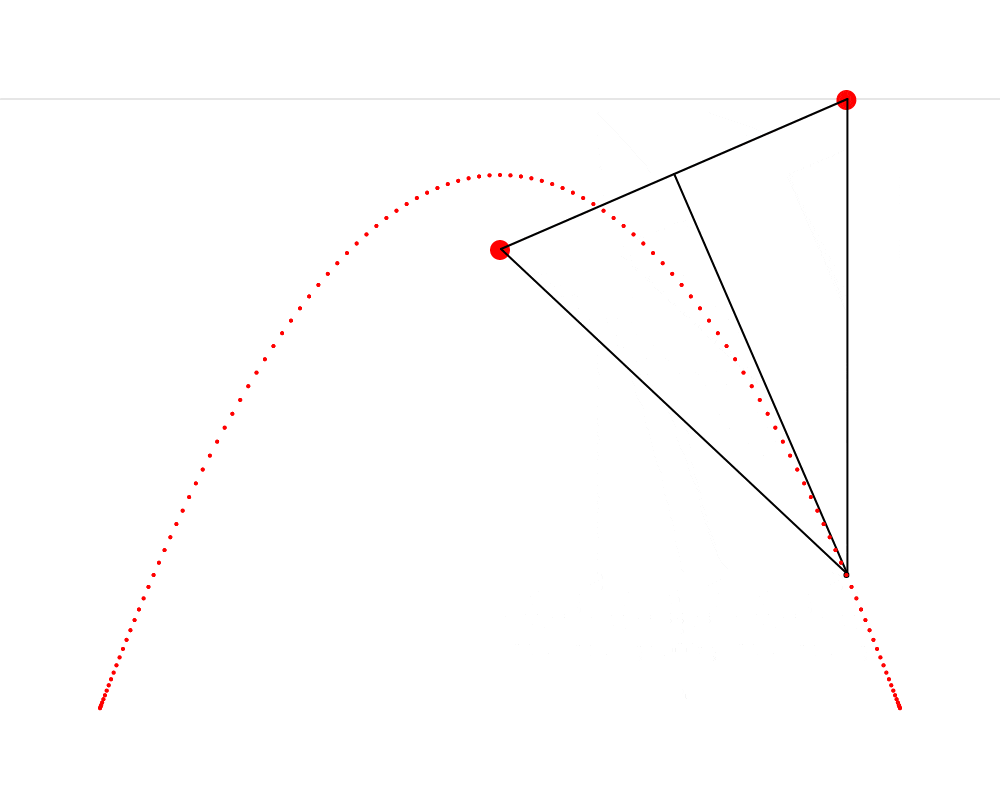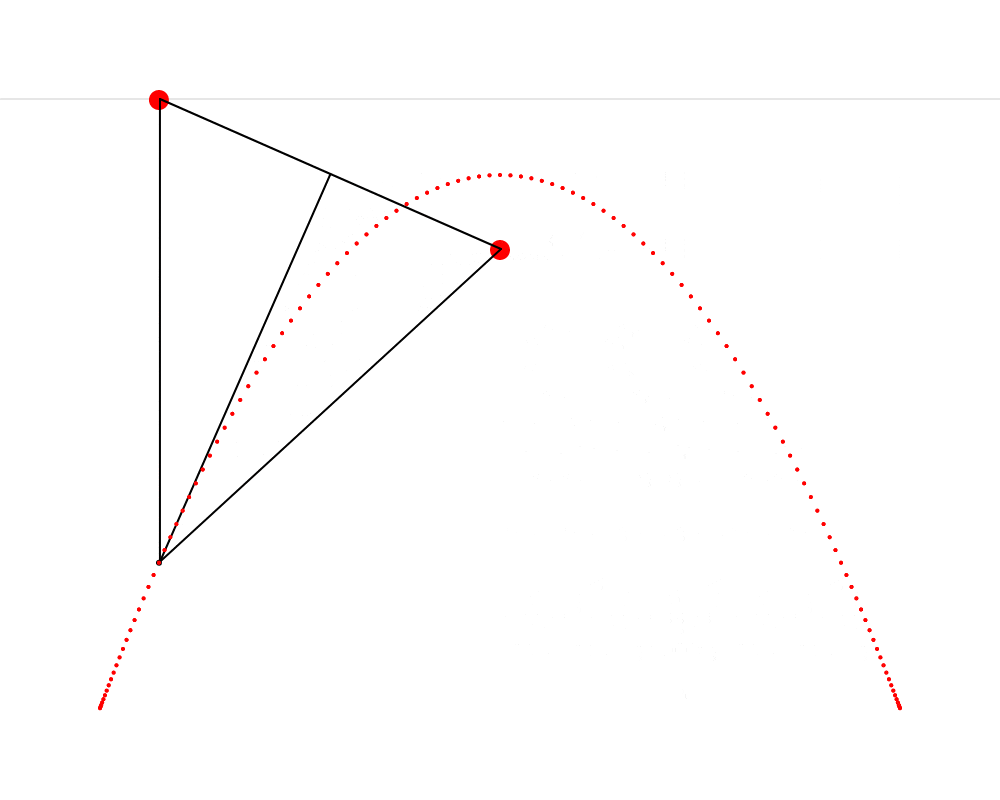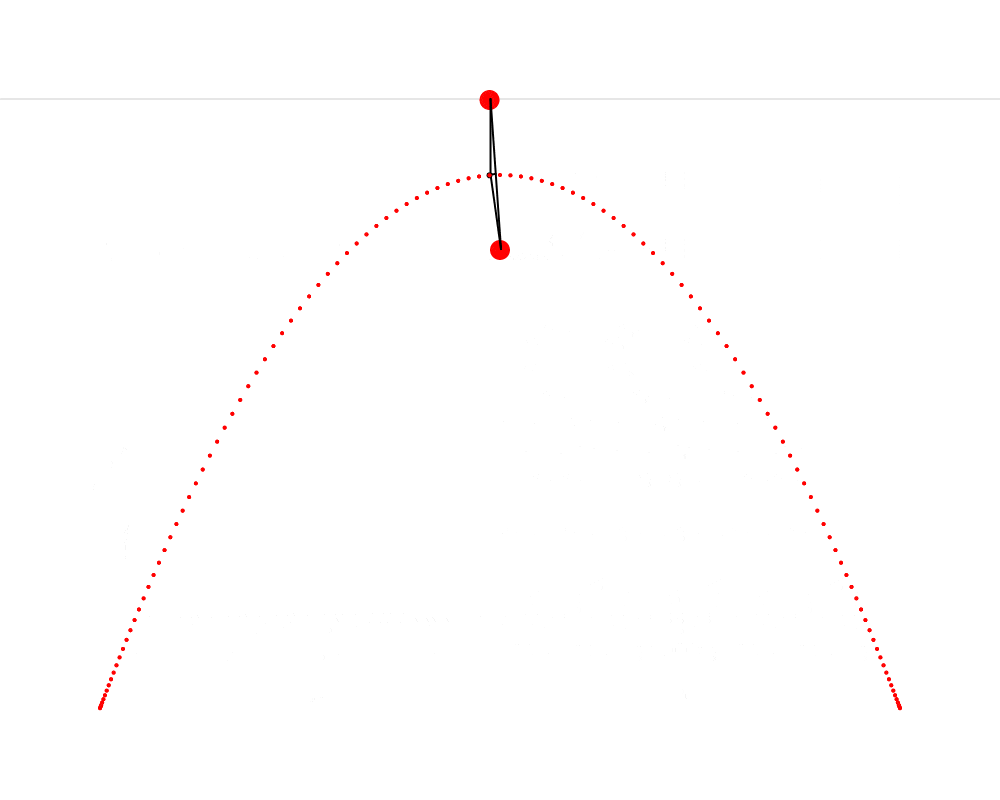
Dans cette animation, nous voyons qu’il est possible de construire un triangle isocèle dont le premier sommet est situé sur une ligne d’horizon, le second sommet est situé près du haut de la montagne, Cet endroit où Hendy nous fait imaginer un champignon s’appelle le foyer de la parabole. Wikipédia décrit une parabole comme étant « une courbe plane dont chacun des points est situé à égale distance d’un point fixe, le foyer, et d’une droite fixe, la directrice. » On constate ainsi que le présent exercice nous fait répliquer très précisément cette définition. et le troisième sommet trace une parabole. J’ai aussi découpé ce triangle isocèle en deux triangles rectangles — je trouvais que cette coupe rendait plus claire la symétrie qui est présente dans le triangle isocèle et qui est ici très importante.

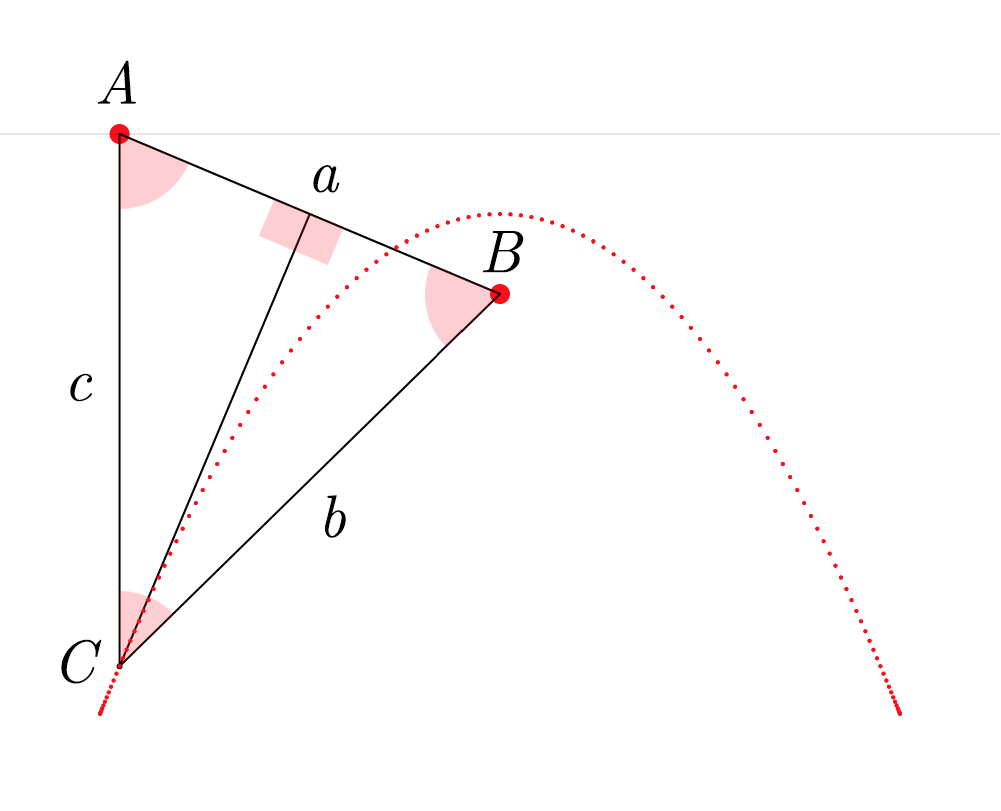
Pour construire ce triangle $ABC$, il faut d’abord projeter une ligne verticale $c$ vers le bas depuis le sommet $A$ et une autre ligne $a$ entre les sommets $A$ et $B$. Ensuite, il faut calculer l’angle $A$ et projeter une ligne $b$ depuis le sommet $B$ de façon à former un angle égal à $A$ (pour que $ABC$ soit isocèle). Les côtés $b$ et $c$ du triangle se croisent finalement au sommet $C$. Lorsque ce processus est répété en partant de plusieurs points sur la ligne d’horizon, les sommets $C$ de tous les triangles obtenus forment une parabole.

Une visite impromptue au royaume des sons

Une des premières choses qui m’est venue à l’esprit après avoir dessiné une parabole était que je pouvais maintenant en créer une quantité infinie de copies et les considérer ensemble comme étant un signal, une onde parabolique.

J’ai tout de suite été curieux d’entendre cette onde. Puisque l’onde parabolique semble avoir des caractéristiques communes avec l’onde sinusoïdale et l’onde triangulaire (la courbe douce de l’une et l’angle acéré de l’autre), j’ai d’abord imaginé que sa sonorité semblerait être à mi-chemin entre ces deux ondes. L’onde parabolique ressemble aussi beaucoup à la valeur absolue d’une onde sinusoïdale, mais elle en est tout de même différente, comme on peut le voir ici. Mon intuition s’est avérée fausse.

Ci-dessous, vous pouvez écouter un fichier sonore qui contient trois notes : un la à 220 Hz joué avec une onde sinusoïdale, puis avec une onde parabolique, et finalement avec une onde triangulaire. On peut remarquer que l’onde parabolique, par sa sonorité, ne semble pas être à mi-chemin entre les deux autres ondes.

Une onde sinusoïdale, une onde parabolique et une onde triangulaire.

0:00

9:00

L’hiver dernier, j’ai commencé à construire un échantillonneur de piano acoustique dans SuperCollider. Les premières versions du projet avaient plusieurs problèmes de fonctionnement et ma connaissance limitée de sclang me rendait la tâche assez ardue. J’ai depuis beaucoup joué avec l’échantillonneur et j’en ai amélioré le code au fil du temps. Je compte encore y travailler sporadiquement mais je me suis dit qu’il était déjà dans un état présentable et qu’il pourrait peut-être servir aux intéressé·e·s. Alors le voici.

L’instrument utilise une collection d’échantillons J’avais utilisé ces mêmes échantillons pour la trame sonore de mon court métrage Étude pour automates cellulaires no. 2. J’avais composé ce morceau avec Ableton Live parce que je ne connaissais pas SuperCollider à ce moment-là. Le morceau n’utilise d’ailleurs qu’un ou deux échantillons différents parce que j’avais constaté que la construction d’un bon échantillonneur avec Ableton Live était grosso modo un cauchemar. J’ai plus tard réutilisé ces échantillons de piano dans cette expérience de programmation en direct qui est un de mes premiers projets réalisés avec SuperCollider.qui est dans le domaine public et que vous pouvez télécharger sur freesound.org. Il vous faudra vous créer un compte pour faire le téléchargement, mais la création d’un compte ainsi que les téléchargements sont gratuits. Il s’agit d’un excellent site Web que je recommande fortement.

Vous trouverez ci-dessous la totalité du code de l’échantillonneur ainsi que deux exemples de Pbind servant à faire une courte démonstration de l’instrument. Il s’agit d’un logiciel libre distribué avec une licence Apache 2.0. Vous pouvez aussi consulter ce code sur GitHub.

// Run this block of code once the server is booted.
// You also need to make sure that the packLocation variable
// is set to the actual location of the downloaded sample pack.

(
var pianoSamples, pianoFolder, makeLookUp, indices, pitches, dynAmnt, maxDyn, maxNote,
packLocation = "/21055__samulis__vsco-2-ce-keys-upright-piano/",
quiet = false;

dynAmnt = if (quiet, {2}, {3});
maxDyn = if (quiet, {1}, {2});
maxNote = if (quiet, {46}, {1e2});
pianoSamples = Array.new;
pianoFolder = PathName.new(packLocation);
pianoFolder.entries.do({
    |path, i|
    if (i < maxNote, {
        pianoSamples = pianoSamples.add(Buffer.read(s, path.fullPath));
    });
});

makeLookUp = {
    |note, dynamic|
    var octave = floor(note / 12) - 2;
    var degree = note % 12;
    var sampledNote = [1,  1,  1,  1,  2,  2,  2,  3,  3,  3,  3,  3];
    var noteDeltas = [-1, 0,  1,  2, -1,  0,  1, -2, -1,  0,  1,  2];
    var dynamicOffset = dynamic * 23;
    var sampleToGet = octave * 3 + sampledNote[degree] + dynamicOffset;
    var pitch = noteDeltas[degree];
    [sampleToGet, pitch];
};
indices = dynAmnt.collect({|j| (20..110).collect({|i| makeLookUp.(i, j)[0]})}).flat;
pitches = dynAmnt.collect({|j| (20..110).collect({|i| makeLookUp.(i, j)[1]})}).flat;

Event.addEventType(\pianoEvent, {
    var index;
    if (~num.isNil, {~num = 60}, {~num = min(max(20, ~num), 110)});
    if (~dyn.isNil, {~dyn = 0}, {~dyn = floor(min(max(0, ~dyn), maxDyn))});
    index = floor(~num) - 20 + (~dyn * 91);
    ~buf = pianoSamples[indices[index]];
    ~rate = (pitches[index] + frac(~num)).midiratio;
    ~instrument = \pianoSynth;
    ~type = \note;
    currentEnvironment.play;
});

SynthDef(\pianoSynth, {
    arg buf = pianoSamples[0], rate = 1, spos = 0, pan = 0, amp = 1, out = 0, atk = 0, sus = 0, rel = 8;
    var sig, env;
    env = EnvGen.kr(Env.new([0, 1, 1, 0], [atk, sus, rel]), doneAction: 2);
    sig = PlayBuf.ar(2, buf, rate * BufRateScale.ir(buf), startPos: spos, doneAction: 2);
    sig = sig * amp * 18 * env;
    sig = Balance2.ar(sig[0], sig[1], pan, 1);
    Out.ar(out, sig);
}).add;
)

// Below are examples of patterns that show how to use the instrument.
// I recommend running both patterns at the same time,
// they are made to complement each other.

(
var key = 62;
var notes = key + ([0, 3, 7, 10] ++ [-5, 2, 3, 9]);
~pianoRiff.stop;
~pianoRiff = Pbind(
    \type, \pianoEvent,
    \dur, Pseq(0.5!1 ++ (0.25!3), inf),
    \num, Pseq(notes, inf),
    \dyn, Pseq([1, 0, 0, 1], inf),
    \amp, Pseq([0.5, 2, 2, 0.5], inf),
    \pan, Pwhite(-0.75, 0.75, inf),
    \rel, 4
).play(quant: [2]);
)

(
var key = 62 + 36;
var notes = key + [2, -5, 0, -2];
~pianoRiff2.stop;
~pianoRiff2 = Pbind(
    \type, \pianoEvent,
    \dur, Pseq([0.25, 1.75], inf),
    \num, Pseq(notes, inf),
    \dyn, Pseq([1, 1, 1, 1], inf),
    \amp, Pseq([0.5, 1, 1, 0.5], inf),
    \pan, Pwhite(-0.75, 0.75, inf),
    \rel, 4
).play(quant: [2]);
)

(
~pianoRiff.stop;
~pianoRiff2.stop;
)

Utilisation de l’échantillonneur

La plupart des utilisateurs de SuperCollider pourront probablement faire usage de l’échantillonneur sans difficulté, mais j’ai pensé qu’il pourrait tout de même être utile de rédiger quelques instructions, particulièrement pour les débutants à qui les projets bien documentés peuvent beaucoup servir. Il s’agit aussi d’une opportunité de parler des multiples décisions prises lors de la création de l’instrument, et des divers moyens par lesquels il pourrait encore être amélioré.

J’ai présentement la vague idée de revisiter certains concepts développés pour mon court métrage Ravines et de les réutiliser dans une pièce audiovisuelle en programmation à la volée que je pourrai jouer en concert. J’aime l’idée qu’une œuvre animée puisse exister ainsi dans une forme malléable, changeante et utilisable dans un contexte performatif, en plus d’exister sous la forme d’un court métrage (c’est-à-dire dans un état statique et définitif).

L’ordinateur que j’utilise pour mes concerts en programmation à la volée est assez lent, et conséquemment je dois simplifier et optimiser beaucoup les algorithmes originaux du court métrage afin qu’ils puissent être animés en temps réel. Travailler avec de telles limitations est en soi un défi assez intéressant. Les animations créées pour Ravines demandaient trop de ressources à l’ordinateur pour pouvoir être rendues en temps réel. Le rendu complet a pris environ 12 heures à faire (pour un film de 4 minutes et demi).

Comme on le voit dans les images ci-haut et ci-bas, j’ai également comme objectif d’intégrer la couleur dans ce projet. J’aime l’apparence crue du noir et blanc de Ravines, mais généralement je préfère travailler en couleur et je souhaite créer des morceaux de concert colorés et chaleureux. Le fond coloré de ces images est une adaptation de l’effet de fumée trouvé ici sur ShaderToy.

Je suis présentement en train d’apprendre les rudiments de la synthèse à tables d’ondes (“wavetable synthesis”) avec SuperCollider, et je vais rassembler ci-dessous mes notes de travail et mes premières esquisses musicales. J’ai commencé mon apprentissage grâce à cette excellente vidéo de Eli Fieldsteel, qui lui-même prend une part de son matériel dans la documentation de la classe Shaper.

Tout commence par la création d’une table d’ondes :

~sig = Signal.newClear(513);
(
~sig.waveFill({
    arg x, y, i;
    // i.linlin(0, 512, -1, 1);
    // sin(x);
    sin(x.cubed * 20);
}, 0, 1);
~sig.plot;
~w = ~sig.asWavetableNoWrap;
~b = Buffer.loadCollection(s, ~w);
)

On crée tout d’abord un Signal, on le remplit avec la méthode waveFill, puis on le transforme en Wavetable, puis en Buffer. L’expression sin(x.cubed * 20) qui remplit le Signal a été écrite arbitrairement après plusieurs essais, et j’aime beaucoup le son qu’elle produit.

En continuant à apprendre la programmation à la volée avec SuperCollider ainsi que l’écriture de shaders WebGL, j’ai composé une nouvelle pièce audiovisuelle. J’ai interprété cette pièce à La Vitrola le 29 mars 2019, lors de la troisième édition de Signes vitaux, une série de concerts organisée par Rodrigo Velasco (Yecto) et Toplap Montréal.

Malheureusement, mon ordinateur n’est pas assez rapide pour faire un rendu de cette pièce, alors il m’est impossible de la partager en ligne pour le moment.

Le code écrit pour réaliser l’animation ci-dessus et celle ci-dessous se trouve sur la branche noise-loops du projet Evolutionary Botany sur GitHub. L’implémentation du bruit OpenSimplex que j’utilise s’appelle SimplexNoiseJS et a été écrite par Mark Spronck.

En apprenant les bases de l’apprentissage automatique, je me suis frappé (bien entendu) à des notions de calcul intégral et différentiel. Je suis très peu familier avec ces notions et j’aimerais beaucoup pouvoir les apprendre en profondeur, à ma façon, c’est-à-dire en créant un ensemble de petites expériences qui pourraient me permettre d’explorer le sujet d’une manière intuitive.

L’animation ci-dessous est une de ces expériences. Elle m’a aidé à me familiariser avec les concepts de limite et de tangente. Une ligne est tangente à un cercle lorsque sa pente est identique à celle du cercle à l’endroit où elle le touche. Cette pente est calculée en prenant deux points différents sur le cercle, et en rapetissant quasi-infiniment la distance entre ces deux points. Écrire le code nécessaire à faire cette animation m’a demandé de faire exactement ceci. J’étais intéressé de voir quelles sortes de formes je pourrais créer en considérant ces notions, et je me suis retrouvé avec cette grille de lignes tangentes également distribuées autour d’un cercle. J’étais ensuite curieux de voir quels mouvements traverseraient cette grille si la forme du cercle était altérée.

J’ai rassemblé ci-dessous des notes que j’ai prises en suivant les tutoriels vidéo de Daniel Shiffman sur les réseaux neuronaux, qui eux-mêmes s’inspirent largement de Make Your Own Neural Network, un livre écrit par Tariq Rashid. Les concepts et les formules ne sont pas de moi, je ne fais que les écrire afin de m’aider à les comprendre et à les mémoriser.

Algorithme de propagation avant

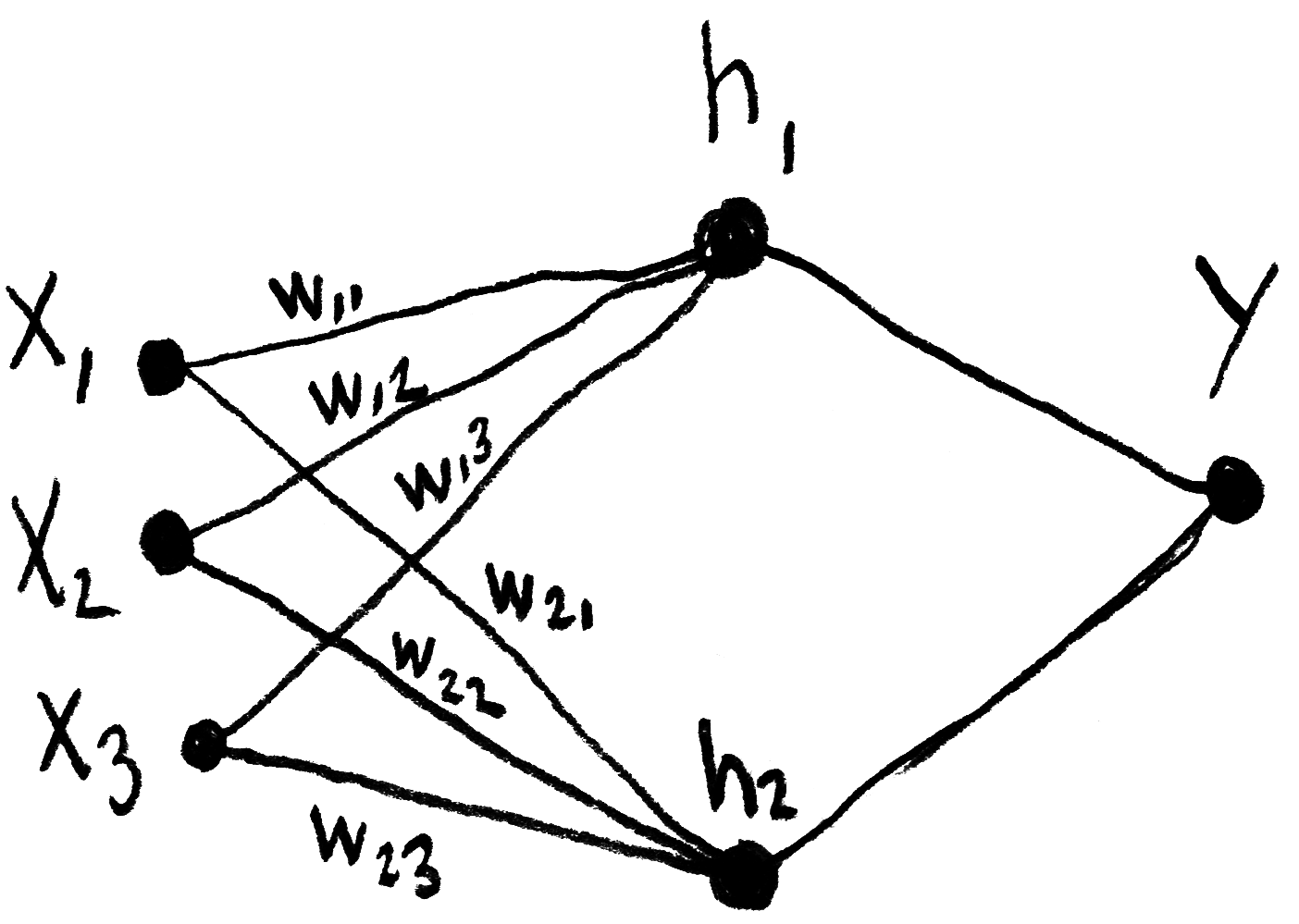
Le calcul réalisé par une des couches du réseau, qui se fait en considérant ses « poids synaptiques » (en anglais, “weights”), peut se résumer par le produit matriciel ci-dessous, dans lequel $h$ représente une des couches intermédiaires (ou « couches cachées ») du réseau, $w$ représente les poids et $x$ représente les nœuds d’entrées (“inputs”) . Dans cette notation inversée, ${\vec{w}}_{ij}$ indique le poids de $j$ vers $i$.

Ce produit peut aussi se représenter ainsi :