Dans ces expérimentations, je cherche différentes façons de créer des séquences d’instructions pour une tortue géométrique. Utiliser du bruit de Perlin (unidimensionnel ou bidimensionnel) me semble être une idée de départ intéressante.

L’animation ci-dessus est une représentation visuelle de la suite de Recáman, qui est une suite d’entiers naturels nommée d’après le mathématicien colombien Bernardo Recamán Santos. J’ai appris l’existence de cette suite dans une vidéo de Daniel Shiffman.

Comme j’aime beaucoup les spirales la première idée qui m’est venue en regardant cette vidéo a été de visualiser la suite en la déployant sur un axe gradué qui aurait la forme d’une spirale.

Suite à la création d’un premier court métrage utilisant les automates cellulaires, de nouvelles expérimentations m’ont fourni le matériel nécessaire à la création d’un second : Étude pour automates cellulaires nº 2, qui se trouve aussi sur YouTube.

Le brillant livre de Melanie Mitchell Complexity: A Guided Tour contient une explication assez exhaustive des algorithmes génétiques, c’est-à-dire des algorithmes qui sont conçus pour pouvoir évoluer en fonction de forces extérieures qui sont appliquées sur eux. Mitchell se sert des automates cellulaires pour construire un exemple de ces algorithmes génétiques. Lors de ma lecture de ce livre, j’ai programmé un système me permettant d’appliquer cette matière fascinante et d’en faire des courts métrages d’animation.

Étude pour automates cellulaires nº 1 est un premier exemple de film d’animation réalisé avec ces méthodes, et il peut être visionné sur YouTube. L’image ci-dessus est tirée de ce film.

Ce malheur qui nous asphyxiait nous avait d’abord semblé doux comme un matin rose en terrain familier.

L'image ci-dessus est tirée d’une animation Une version basse résolution de cette animation se trouve sur mon fil Twitter. générée par un programme que je suis en train d’écrire. L’image a été formée par des automates cellulaires, c’est-à-dire que chacune des cases colorées que l’on voit répond à un ensemble de règles qui modifient ses propriétés.

Je compte rassembler une collection de ces animations afin d’en faire un court métrage ainsi qu’une bande dessinée composée d’images fixes. J’ai publié une esquisse du projet de bande dessinée dans le premier numéro de la revue Colère, un journal de création qui contient aussi des merveilleux travaux d’Alexa Perchemal, de Mirion Malle, de Sophie Bédard et de Saturnome. Les pages ont également été publiées dans le troisième numéro du zine Seeds, une publication annuelle dédiée à l’art procédural et éditée par Jupiter Hadley et Dann Sullivan.

Il me faut construire un phénotype complet ; pour l’instant, je n’en ai qu’un prototype. Il me faut tout d’abord séparer la définition du phénotype et son interprétation. Son interprétation doit être séparée, elle ne doit pas être une méthode du prototype DNA.

Une chose un peu complexe : je veux avoir plusieurs types d’adn, mais également plusieurs façons d’exprimer un type d’adn.

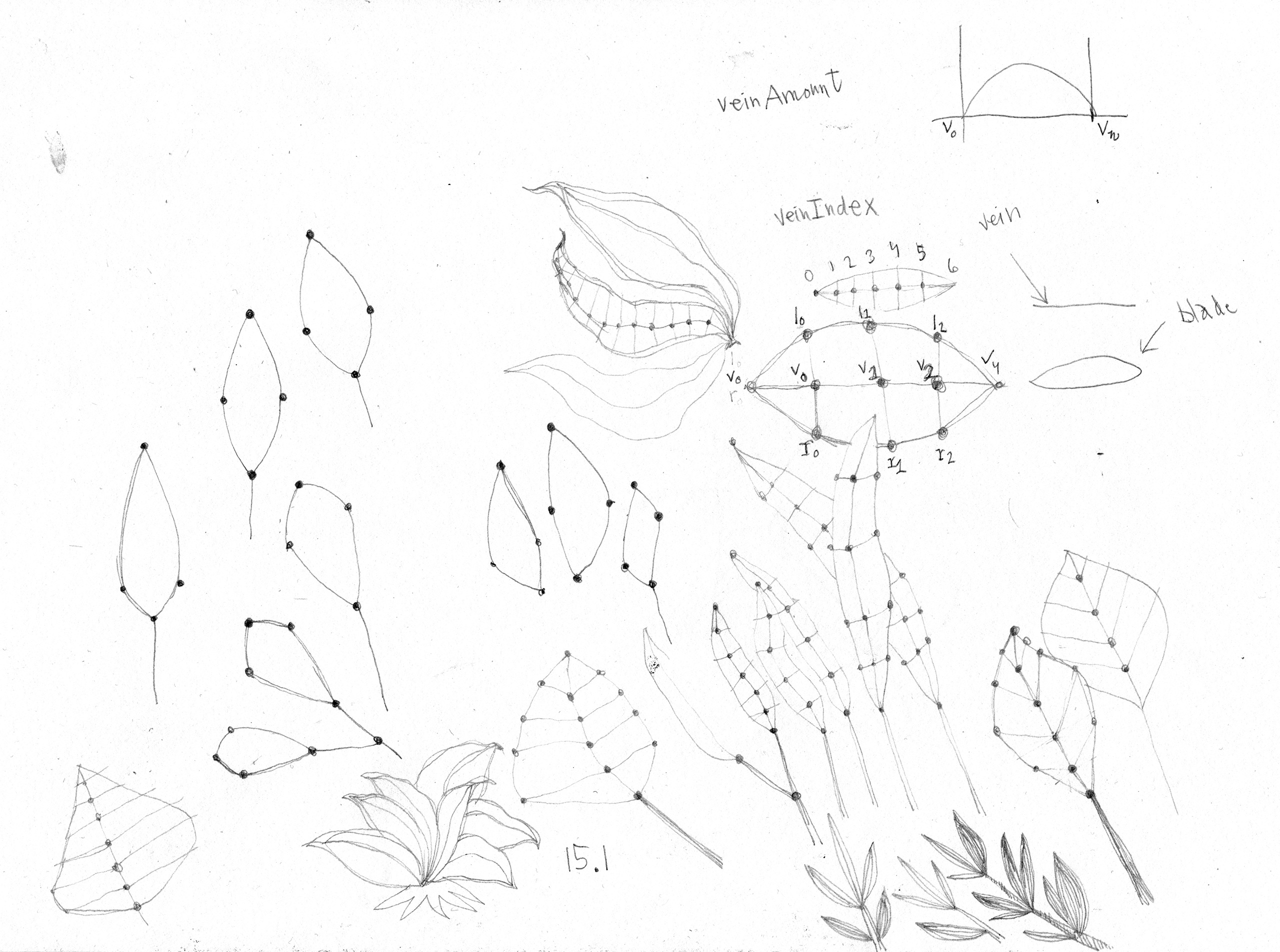
Un jardin sans feuillage serait d’une tristesse accablante. Je suis donc en train de construire un système avec lequel je pourrai affubler mes branches artificielles de différents types de feuillage. Ce faisant, j’ai pris beaucoup de notes très techniques et qui ne seront pas nécessairement digestes pour quiconque, mais je les partage tout de même ci-dessous, afin de documenter mon processus.

Les croquis ci-dessus proviennent des mêmes recherches. Ce travail a aussi mené à la création d’une première animation, partagée sur mon fil Twitter.

Le rêve vers lequel tendent mes recherches sur la botanique algorithmique est de créer des scènes botaniques complètes, avec couleurs, feuillages, perspective atmosphérique, mouvements venteux dans les branches, etc. Pour tout dire, ça ne déplairait pas de devenir le Henri Rousseau de l’art algorithmique… Je suis loin d’en être là, mais j’y travaille. J’ai rassemblé ci-dessous plusieurs notes prises lors de l’élaboration d’un système qui me permettrait de gérer des scènes avec de multiples végétaux distribués dans un tableau.

ravailler sur le système d’embranchements déterministes dont je parle dans ma note de blog précédente m’a amené à créer la petite animation ci-dessus. J’utilise dans mon système la fonction cosinus afin de créer des branches courbées, et pour tester l’effet de cette fonction sur une branche en pleine croissance, j’ai isolé le problème en faisant marcher une tortue géométrique sur le parcours du cosinus.

J’ai été très surpris des résultats de cette petite expérience. Je m’attendais à ce que le parcours de la tortue ressemble simplement à une onde sinusoïdale, mais la tortue produit en réalité un grand ensemble de parcours différents selon la fréquence à laquelle est appliquée la fonction cosinus. Afin de bien illustrer le phénomène, j’ai indiqué, dans le coin inférieur gauche de l’animation, à quelle fréquence le cosinus est appliqué lors de chacune des marches de la tortue.

Je veux créer un système d’embranchements pour mon système de botanique algorithmique qui ne repose pas sur le hasard, de façon à ce que mes algorithmes génétiques puissent déterminer quels sont les types d’arbres les plus « performants » (je ne sais toujours pas comment ces performances pourront être évaluées).

Mon système d’embranchement m’a permis de créer une grande quantité d’arbres différents ; chaque arbre possède clairement une apparence, ou un caractère visuel, qui lui est propre. On peut voir un montage de plusieurs de ces arbres en croissance sur mon fil Twitter.

J’ai rassemblé ci-dessous beaucoup de notes techniques prises lors de ce travail.