Les pavages de Truchet

Premiers pas vers les pavages

Les pavages ci-dessus ont été générés par un programme que j’ai écrit avec JavaScript et la bibliothèque p5.js. Ils sont le produit d’un hasard contrôlé : je n’ai pas choisi les palettes de couleur ni la position des triangles et des rectangles dont ils sont faits. J’ai plutôt créé les conditions permettant leur création.

Pour réaliser ce projet, je me suis inspiré des travaux de Sébastien Truchet, un mathématicien et ingénieur français qui œuvrait au début des Lumières. En 1704, Truchet écrivit un Mémoire sur les combinaisons qui présente ses recherches sur les pavages. Ce Mémoire apparaît à la page 363 de l’Histoire de l’Académie royale des sciences, un ouvrage disponible gratuitement sur Gallica, un site Web de la Bibliothèque nationale de France. Vous pouvez aussi y trouver un bel ouvrage écrit par le mathématicien Dominique Doüat en 1722, Méthode pour faire une infinité de desseins différens. Doüat reprend les idées de Truchet et présente de nouveaux pavages. Il y relate un voyage à Orléans durant lequel il trouva dans un château « plusieurs carreaux de faïence carrés et mipartis de deux couleurs par une ligne diagonale, qui étaient destinés à carreler une chapelle et plusieurs autres appartements. »

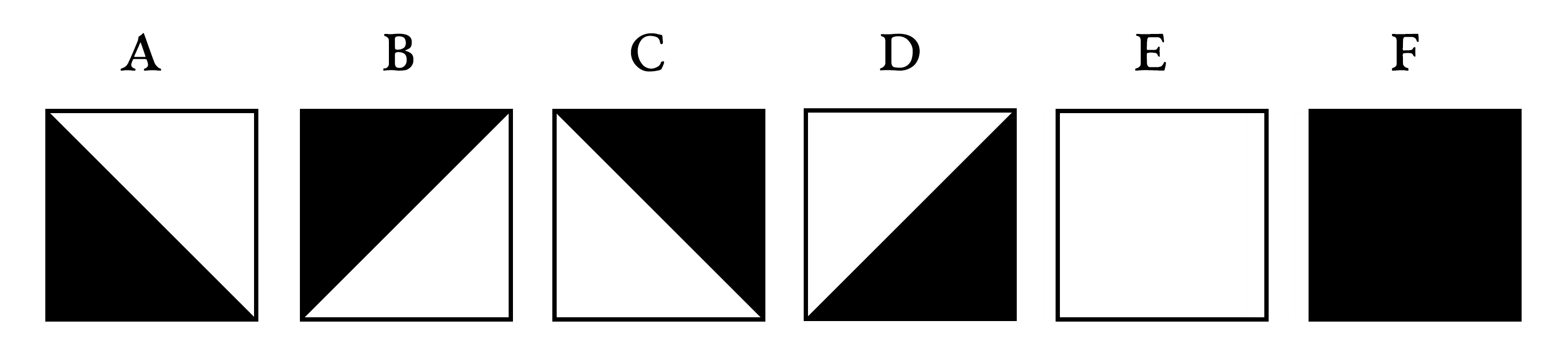
Les carreaux que Truchet décrit sont tous identiques et peuvent être tournés sur eux-mêmes en quatre positions différentes, qu’il désigne a, b, c et d :

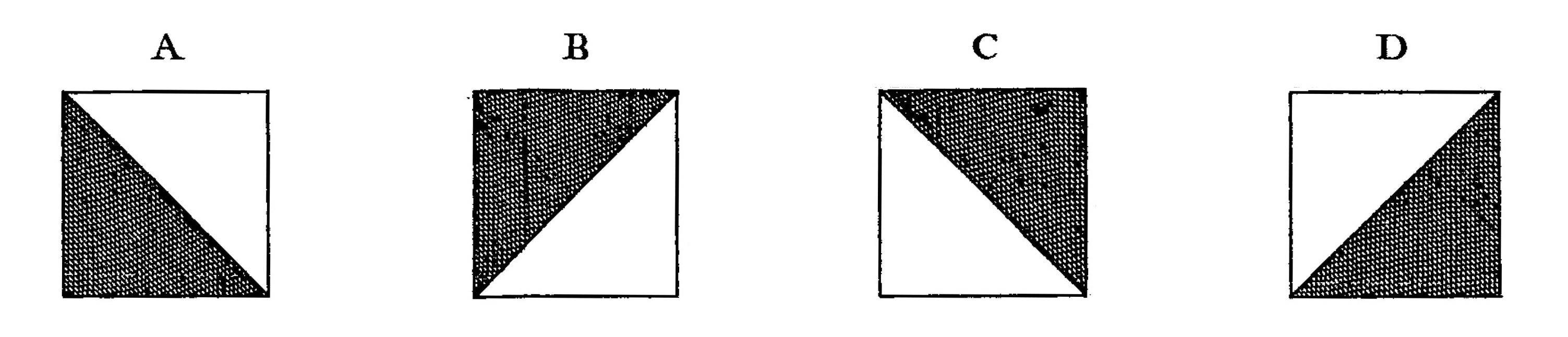
Truchet continue : « Pour pouvoir former des dessins et des figures agréables par l’arrangement de ces carreaux, j’examinai d’abord en combien de manières deux de ces carreaux pourraient se joindre ensemble, en les disposant toujours en échiquier. » Il présente ensuite les figures qui résultent de ces combinaisons, puis celles qui résultent de combinaisons de plus en plus élaborées. Voici quelques-unes des superbes planches qui accompagnent son Mémoire, gravées par Louis Simonneau :

Dans ces planches, on voit que Truchet s’intéresse à la création de groupes symétriques de carreaux. Puisque les positions différentes d’un carreau sont obtenues par des rotations, elles sont aussi liées par des symétries. La position a est liée à b par une symétrie à l’axe horizontal, à c par une symétrie à l’axe diagonal, et à d par une symétrie à l’axe vertical :

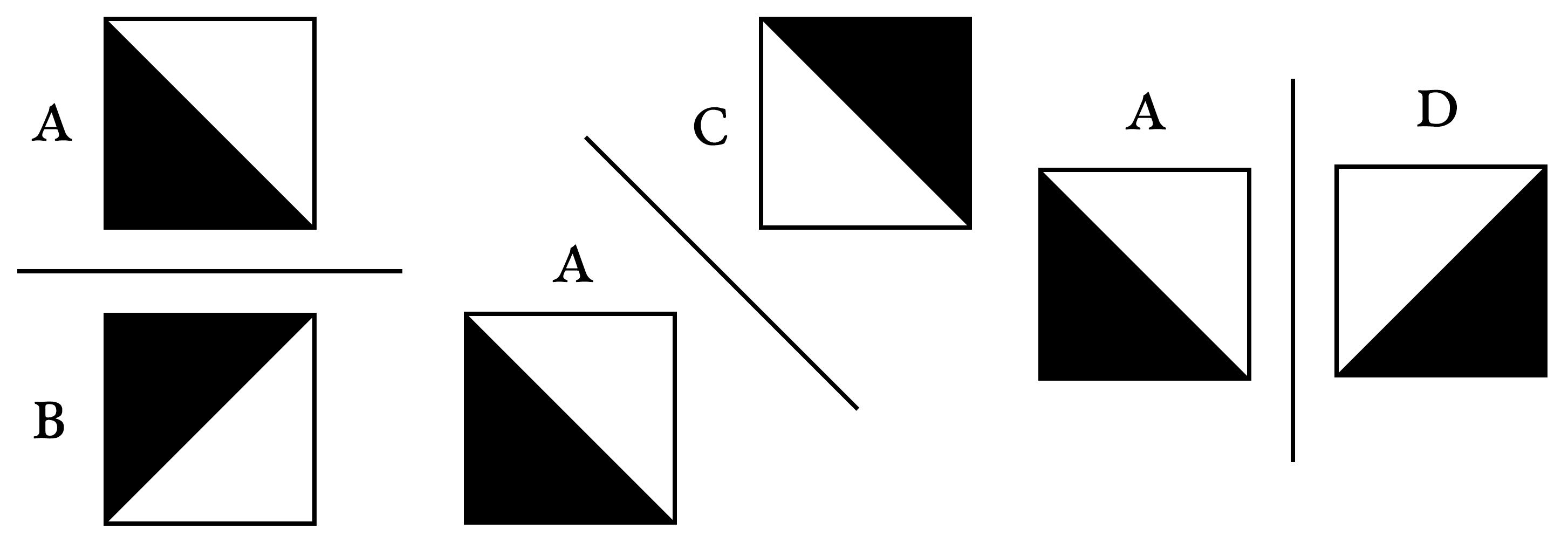
De la même façon, des groupes de carreaux peuvent être liés par symétrie :

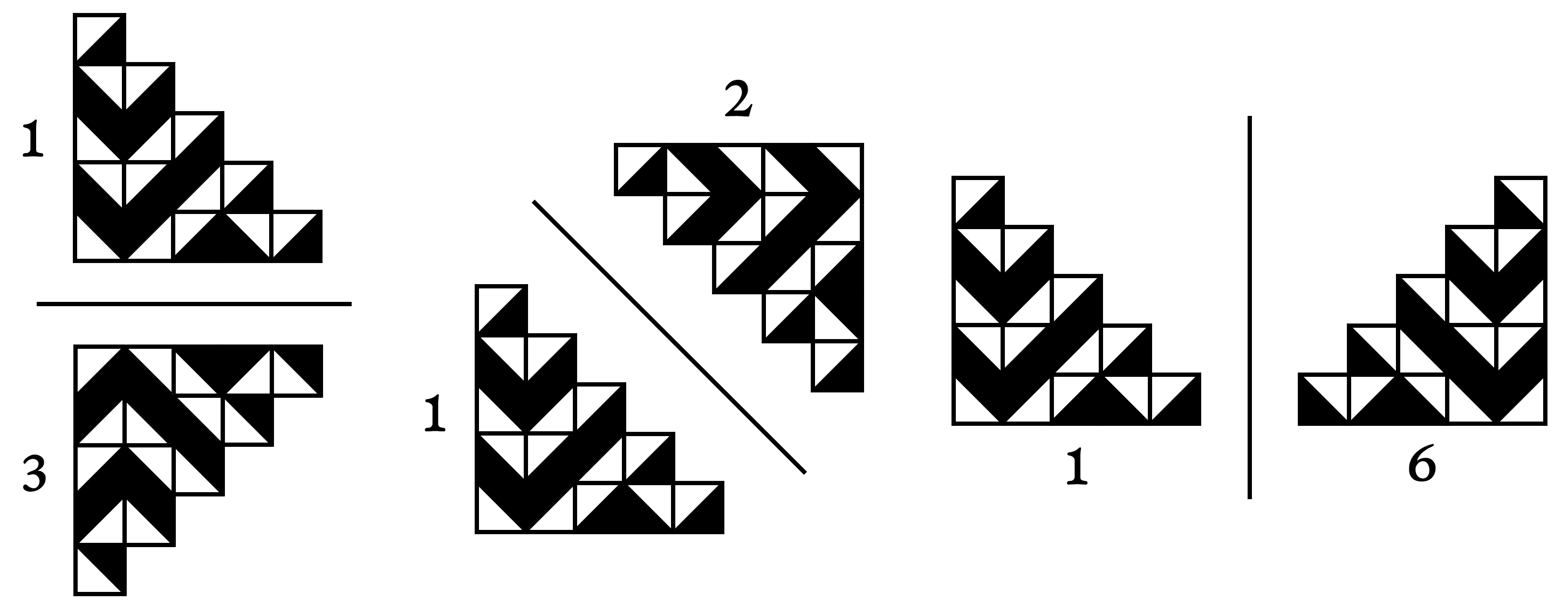
Le groupe en forme d’escalier qu’on voit ci-dessus est crucial pour Truchet, qui s’en sert pour construire la plupart de ses pavages les plus élaborés. Le groupe 1 est simplement copié en versions réfléchies horizontalement, verticalement et diagonalement, de façon à remplir un groupe carré, qui est ensuite lui-même répété dans tout le pavage :

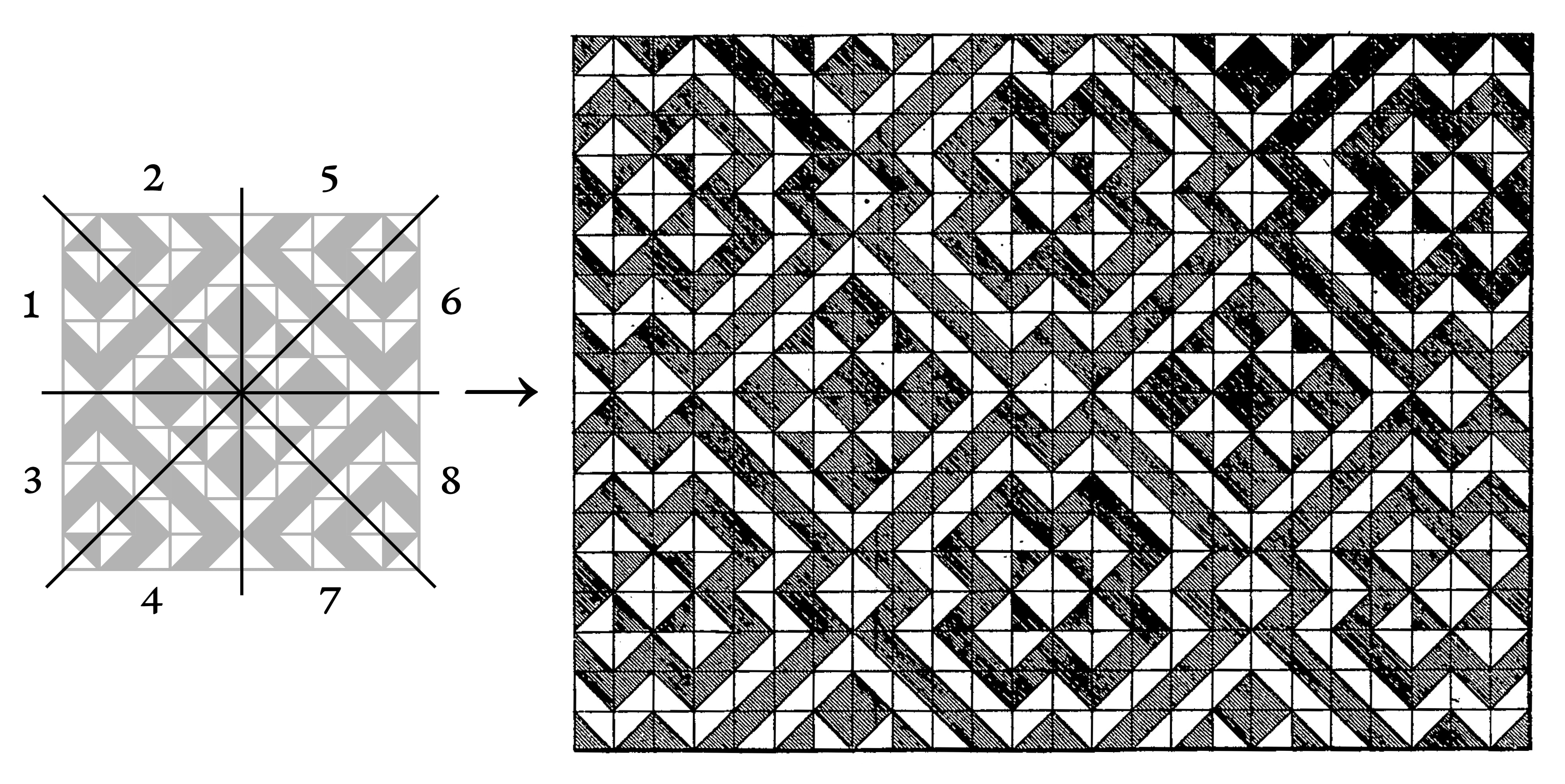
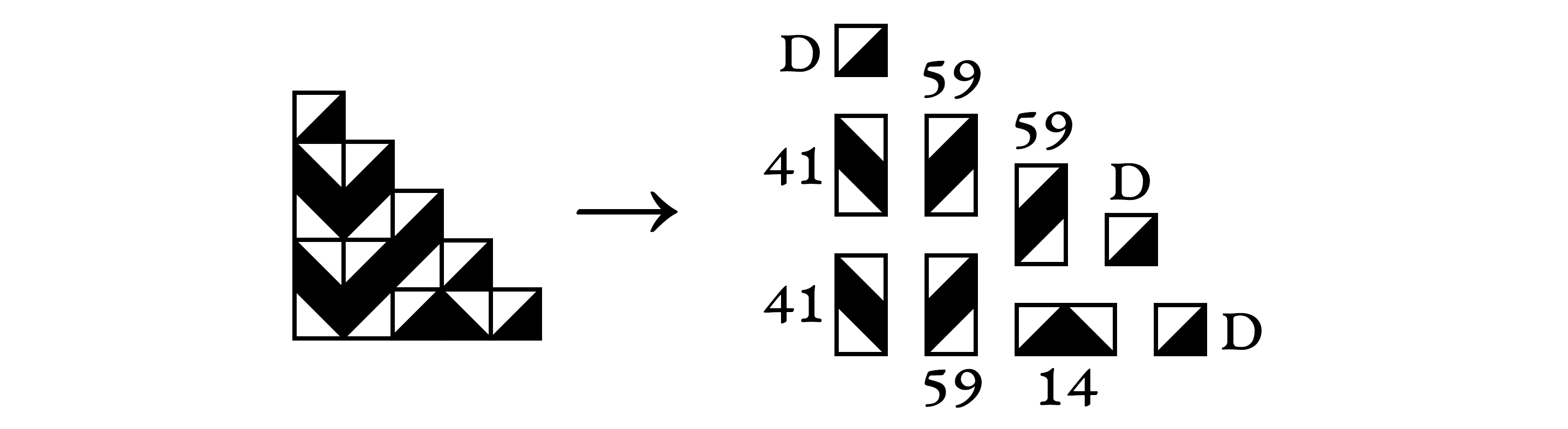
Vous remarquerez que les axes de symétrie qui sont diagonaux passent au milieu des “marches” de l’escalier. Ces marches ne sont donc pas copiées diagonalement dans le pavage. Il est aussi intéressant d’observer que Truchet construit ses escaliers en répétant des combinaisons de plus petits groupes. Sa table 1 (reproduite plus haut) numérote chacune des 64 combinaisons possibles de 2 carreaux. On voit que cet escalier est construit avec les combinaisons suivantes :

Le générateur de pavages aléatoires

En voyant la simplicité des groupes en forme d’escalier que Truchet utilise pour bâtir ses pavages, j’ai décidé d’écrire un programme qui choisirait au hasard chacun des carreaux d’un escalier puis créerait automatiquement toutes les symétries nécessaires au remplissage d’un pavage. J’ai aussi ajouté deux nouveaux carreaux : le carreau vide et le carreau plein, désignés respectivement e et f. La lectrice attentive et le lecteur appliqué comprendront que je triche, puisque a, b, c et d désignent 4 positions différentes du même carreau tandis que e et f désignent 2 carreaux distincts. Me pardonnera-t-on un tel laisser-aller dans la nomenclature ? Je trouve que ces ajouts produisent des motifs qui font varier de manières intéressantes les idées de Truchet.

Instructions pour le générateur : Cliquez ou appuyez sur le pavage ci-dessous pour en générer un nouveau. La touche r de votre clavier produit le même effet. Vous pouvez continuer à utiliser ce mode manuel ou opter pour le mode automatique qui affiche un nouveau pavage à chaque seconde.

Vous pouvez également choisir entre trois ensembles de carreaux à utiliser lors des générations : {a, b, c, d}, {a, b, c, d, e, f} ou {e, f}.

L’étendue des possibles

Une chose surprenante à propos des pavages de Truchet est l’énorme quantité de combinaisons possibles. Par exemple, un pavage dont l’escalier possède une largeur de cinq carreaux peut être assemblé en plus de soixante milliards de combinaisons différentes. Précisément, ce pavage a $61917364224$ combinaisons possibles, ou $6^{10}\times 4^5$. Le diagramme ci-dessous indique le nombre de valeurs possibles pour chacun des carreaux. 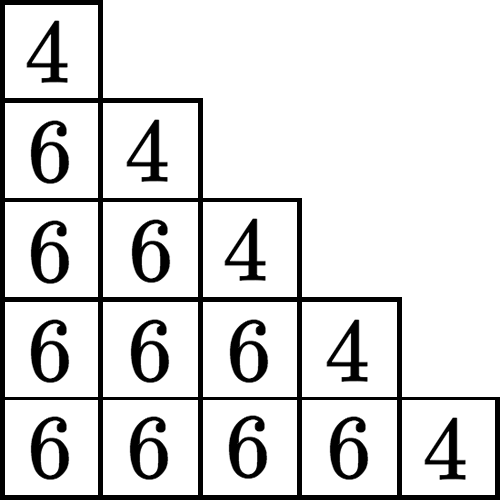Il suffit de multiplier toutes ces possibilités pour obtenir la quantité de combinaisons possibles. Certains carreaux sont limités aux $4$ formes qui sont diagonalement symétriques avec elles-mêmes : {b, d, e, f}. Cette limitation n’est pas obligatoire mais elle forme généralement des pavages plus harmonieux, surtout dans un contexte où les carreaux sont choisis aléatoirement. Si vous cliquiez pour générer un nouveau pavage à chaque seconde sans arrêt, il vous faudrait environ 1 900 ans pour les voir tous (chose que je ne recommande pas). Et comme le générateur crée des pavages dont la largeur de l’escalier varie entre trois et neuf carreaux, le temps nécessaire pour en épuiser les possibilités à ce rythme est près d’un trillion d’années (le chiffre 1 suivi de 18 zéros). Ainsi, chaque pavage qui est généré n’a presque certainement jamais été vu par quiconque avant vous, et vous ne le reverez plus jamais après le prochain clic.

À quoi pourraient ressembler ces pavages si leurs carreaux avaient une apparence différente mais que toutes leurs autres propriétés étaient conservées (symétrie, assemblage par escalier, etc.) ? Par exemple, l’apparence des carreaux pourrait être altérée de cette façon :

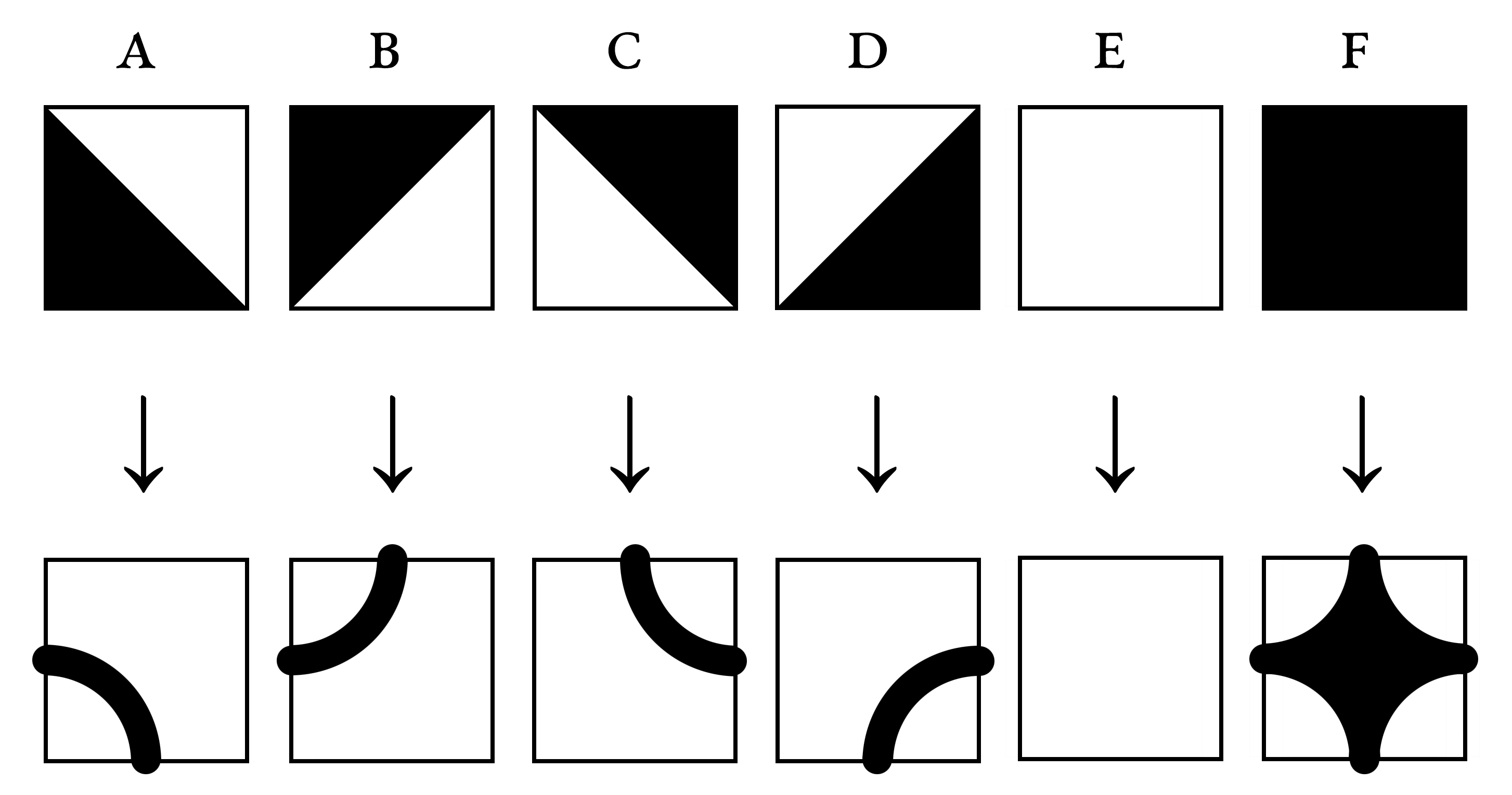
Pour tester ces nouvelles formes dans le générateur, vous pouvez alterner entre le mode angulaire et le mode ondulé et y retourner pour voir les changements. Essayez ce nouveau mode avec l’ensemble complet des carreaux ({a, b, c, d, e, f}) pour les plus beaux résultats. Vous remarquerez aussi que l’épaisseur des lignes courbes change d’une génération à l’autre, parce que ça fait plus joli.

Pavages multicolores

Une des questions à laquelle je souhaitais répondre avec ce projet était : Comment les pavages de Truchet pourraient-ils être colorés ? Afin que la coloration de ces pavages puisse répondre harmonieusement à leur construction symétrique, j’ai décidé d’utiliser la forme en “escalier” qui les structure et de ne colorer que celle-ci.

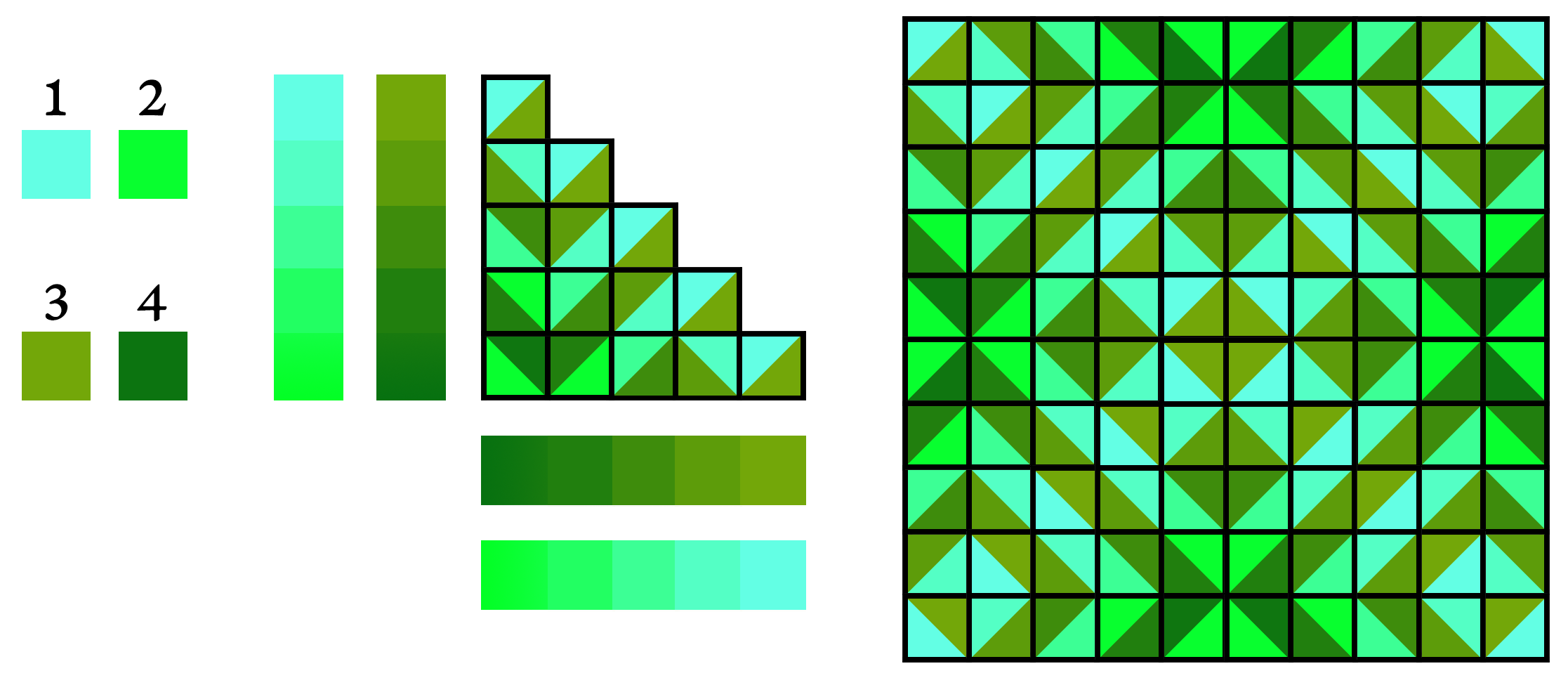
Pour ce faire, j’ai créé un système qui choisit quatre couleurs au hasard à chaque génération d’un escalier. Les couleurs 1 et 2 sont assignées à la partie claire des carreaux, et les couleurs 3 et 4 à la partie foncée. Les couleurs sont ensuite appliquées sur l’escalier, créant un dégradé qui passe de la couleur 1 à la couleur 2, et un autre de la 3 à la 4. Quand l’escalier est réfléchi et copié pour former le pavage, les couleurs obtenues sont ainsi réparties avec les mêmes symétries horizontales, verticales et diagonales.

Puis, afin de donner une légère texture aux pavages, le générateur ne dessine pas réellement les triangles et les carrés qui forment le pavage ; il dessine plutôt des milliers de points colorés à l’intérieur des limites de chaque carreau. Un pavage entier est constitué d’environ 15 millions de points.

Je n’ai pas inclus le générateur de pavages colorés sur cette page parce que la majorité des palettes de couleur qu’il génère sont plutôt dissonantes (après tout, elles sont déterminées complètement par le hasard). De plus, un pavage dessiné avec des millions de points prend plusieurs longues minutes à apparaître. Néanmoins, si vous êtes d’une patience et d’un courage à toute épreuve, vous êtes les bienvenu·e·s à essayer le générateur coloré par vous-mêmes.

Pour les autres, voici quelques pavages colorés générés en janvier 2018 :

Suites possibles

Les pavages forment un énorme domaine mathématique, et il y a beaucoup de nouvelles avenues que j’aimerais emprunter pour faire suite à ce projet. En voici quelques-unes :

• —  Créer un générateur qui construirait les “escaliers” qui sont au cœur des pavages de Truchet d’une manière qui ressemblerait davantage aux méthodes que Truchet utilisait lui-même. Pour l’instant, chaque carreau d’un escalier est choisi complètement au hasard, indépendamment des carreaux adjacents. Comme on le voit dans son Mémoire sur les combinaisons, Truchet formait plutôt ses escaliers en choisissant quelques combinaisons de carreaux et en les répétant plusieurs fois. Les pavages créés ainsi sont plus souvent harmonieux.
• —  Explorer des types de pavages plus complexes, tels que les pavages pentagonaux ou les pavages de Penrose. Je suis particulièrement intéressé par les fascinants pavages découverts par Marjorie Rice en 1976 et 1977. Je vous encourage fortement à en apprendre sur Rice si vous ne la connaissez pas déjà. C’était une femme brillante qui a réussit, sans avoir eu l’opportunité de poursuivre les études universitaires en mathématiques dont elle rêvait, à découvrir de nouveaux types de pavages pentagonaux qui avaient éludé les chercheurs académiques.
• —  Mélanger les automates cellulaires avec les pavages de Truchet. De tels automates pourraient fonctionner avec des règles considérant les états de a à f. Quelles pourraient être ces règles ? Serait-il possible de préserver les symétries qui sont si caractéristiques au travail de Truchet ?
• —  Créer des pavages animés. À quoi pourrait ressembler un film d’animation constitué de pavages en mouvements ? En existe-t-il de bons exemples ?

Licences et usages

Le travail réalisé pour ce projet est distribué avec des licences libres. Vous êtes libres de le redistribuer, de le modifier et d’en distribuer des versions modifiées, si vous respectez les conditions suivantes : vos versions modifiées doivent également être distribuées avec une licence libre et doivent indiquer le nom de l’auteur de l’œuvre originale. Pour plus de détails, veuillez consulter les licences elles-mêmes :

• —  Cette page Web (incluant le texte et les images) est distribuée avec une Licence Art Libre 1.3. Les images tirées du Mémoire sur les combinaisons de Sébastien Truchet font bien entendu partie du domaine public.
• —  Le générateur de pavages en noir et blanc affiché sur cette page Web est distribué avec une licence Gnu Gpl 3.0. Le générateur de pavages colorés est distribué avec la même licence.

Sources

J’ai appris l’existence du Mémoire sur les combinaisons de Sébastien Truchet et de la Méthode pour faire une infinité de desseins différens de Dominique Doüat (qui m’a aussi été d’une grande utilité) grâce aux recherches de Jacques André, un mathématicien et typographe français. Un document pdf qui présente ses recherches est disponible sur son site Web et distribué avec une licence libre.